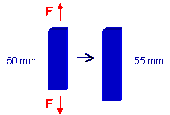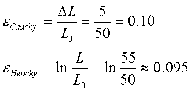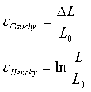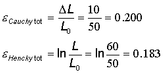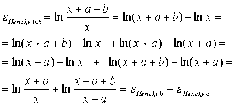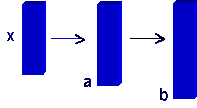Strain
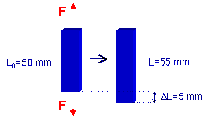
There are different definitions of strain of which Cauchy stain and Hencky strain are most commonly used. The definitions are clearly demonstrated in extension. Cauchy strain is intuitive and defined as the ratio of the extension to the original length as εCauchy=ΔL/L0. Hencky strain is instead defined as εHencky=ln(L/L0).
At infinitesimally small strain εCauchy = εHencky. Hencky strain is in contrast to Cauchy strain additive and the preferred strain definition to use for large strain.
Exercise, calculate strain
A rod is subjected to a tensile force F and extends from 50 mm to 55 mm. Calculate Cauchy strain and Hencky strain.
.
Exercise, calculate strain
A rod is subjected to a tensile force F and extends from 50 mm to 55 mm. Calculate Cauchy strain and Hencky strain.
.
.
Exercise, calculate strain
A rod is subjected to a tensile force F and extends from 50 mm to 55 mm. Calculate Cauchy strain and Hencky strain.
.
Exercise additive strain
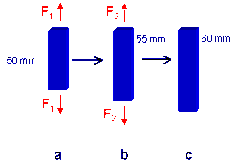
A rod is subjected to a tensile force F1 and extends from 50 mm to 55 mm. Then another tensile force F2 extends the rod to 60 mm. Calculate the extensions in b and c according to Cauchy strain and Hencky strain.
.
.
Exercise additive strain
A rod is subjected to a tensile force F1 and extends from 50 mm to 55 mm. Then another tensile force F2 extends the rod to 60 mm. Calculate the extensions in b and c according to Cauchy strain and Hencky strain.
.
Exercise additive strain
A rod is subjected to a tensile force F1 and extends from 50 mm to 55 mm. Then another tensile force F2 extends the rod to 60 mm. Calculate the extensions in b and c according to Cauchy strain and Hencky strain.
Total extension:
If you add the strain in b and c the total strain is independent of how you calculate it while Cauchy strain depend on how it is calculated. Call the original length x and the incremental extensions for a and b, then